Inleiding
Door de eeuwen heen hebben wiskundigen, kunstenaars, architecten en filosofen gezocht naar patronen die de orde van de wereld weerspiegelen. Twee van de meest intrigerende concepten zijn de Gulden Snede en de Fibonacci Reeks1. Beide drukken een gevoel van harmonie en evenwicht uit.
De Gulden Snede: de maat van harmonie
De Gulden Snede wordt aangeduid met de Griekse letter φ (phi), en is een getal van ongeveer 1,6180339.
De verhouding ontstaat wanneer een lijnstuk zó wordt verdeeld dat de verhouding tussen het geheel (a+b) en het grootste deel (a) gelijk is aan de verhouding tussen het grootste (a) en het kleinste deel (b).
Wiskundig: (a+b) / a = a / b = φ
De Griekse wijsgeer Euclides beschreef als eerste het getal φ, maar men gebruikte de Gulden Snede waarschijnlijk al eerder. De oude Egyptenaren bouwden hun piramides op basis van de Gulden Snede.
φ is ook op andere plaatsen te ontdekken: bijvoorbeeld in de verhouding tussen de lengte van het middelste botje in je vinger tot het langste botje en het kortste botje. Ook in het hartslagpatroon – zichtbaar gemaakt op een ECG – is tussen de hartslagen de verhouding van φ terug te vinden.
De Fibonacci-reeks
De Fibonacci-reeks is een getallenreeks die begint met 0 en 1, waarna elk volgend getal de som is van de twee voorgaande:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Wat de reeks zo bijzonder maakt, is dat de verhouding tussen opeenvolgende getallen steeds dichter nadert tot φ (van de Gulden Snede). Met andere woorden: de Fibonacci Reeks is gerelateerd aan de Gulden Snede.
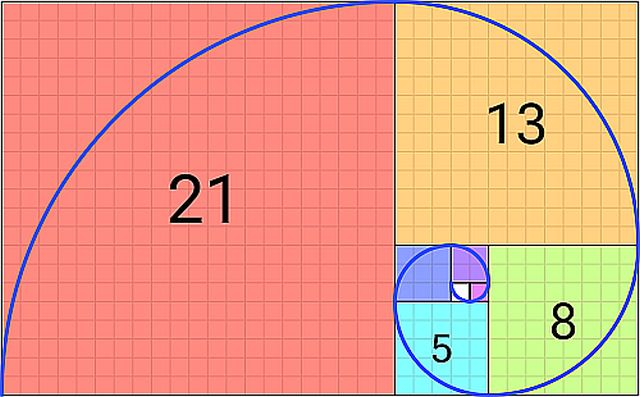
De Fibonacci Reeks zit vol met eigenaardigheden, zoals elke optelsom van tien opeenvolgende getallen uit de reeks is deelbaar door elf. Om de zestig getallen herhaalt het laatste cijfer, bijvoorbeeld het tweede getal is 1, het tweeënzestigste getal in de reeks eindigt op een 1 (….4052739537881), het 122ste getal in de reeks eindigt op een ….. 1 (…..14028366653498915298923761), etcetera.
Natuur als bewijs van universele orde
Zowel de Gulden Snede als de Fibonacci Reeks duiken overal in de natuur op:
- De spiralen van zonnebloemen volgen vaak Fibonacci-patronen (meestal tel je 34 spiralen die de ene kant op wijzen en 55 die de andere kant op wijzen).
- De verhouding tussen de segmenten van zeeschelpen benadert φ.
- De verdeling van bladeren rond een stengel (zogenaamde phyllotaxis) volgt vaak Fibonacci-hoeken, zodat elke blad zoveel mogelijk licht opvangt.
Deze regelmatigheden suggereren dat de natuur “economisch” werkt en dat de Gulden Snede een optimale verhouding is voor groei en verspreiding.

Ook in kunst en architectuur
Kunstenaars en architecten hebben door de eeuwen heen de Gulden Snede bewust toegepast:
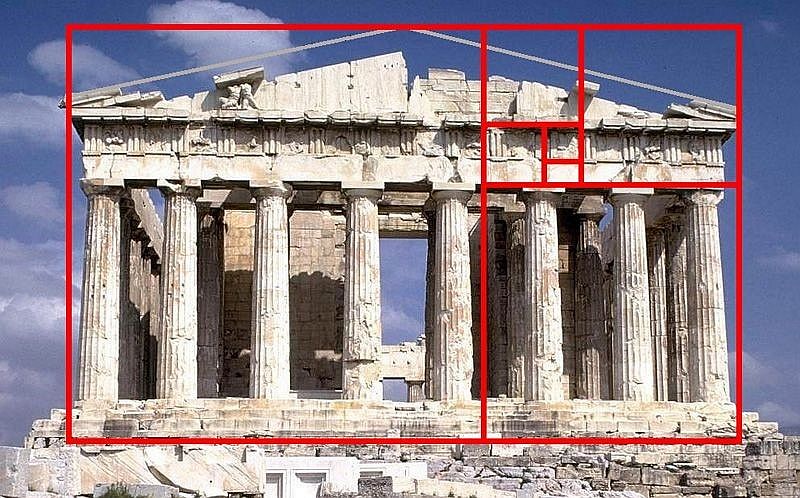
- De verhoudingen van de Parthenon-tempel in Athene zouden ontworpen zijn volgens φ.
- Leonardo da Vinci gebruikte de gulden snede bij zijn illustratie van de Vitruviusman en mogelijk in de compositie van de Mona Lisa.
- In de moderne kunst gebruikte Piet Mondriaan verhoudingen die φ benaderen in zijn abstracte werken.
De vraag die we hierbij kunnen stellen: is het gebruik van φ een bewuste keuze van de maker, of herkennen wij achteraf deze harmonie omdat ons oog er gevoelig voor is?
En in muziek
Ook andere kunsten zien de Gulden Snede langskomen. De muziekkunst kan niet zonder de beroemde Fibonacci Reeks. De opbouw van de pianotoetsen volgt bijvoorbeeld de reeks. Een octaaf op een piano wordt gespeeld met 8 witte toetsen en 5 zwarte, in totaal dus 13 toetsen. De zwarte toetsen zijn verdeeld in twee en drie. Dat is dus de Fibonacci Reeks: 2, 3, 5, 8, 13!
Volgens sommigen te ver gezocht en gewoon toeval, maar anderen geloven er heilig in. Componisten zoals Bartók en Debussy hebben de Fibonacci Reeks (bewust of onbewust?) in hun werk verstopt.
In uiterlijk
Niet alleen in de kunst kom je φ tegen, ook menselijke schoonheid volgt de wetten van de Gulden Snede. In het menselijke gezicht vind je allerlei verhoudingen die de Gulden Snede benaderen. Bijvoorbeeld de verhouding van de lengte van je neus tot de breedte. Of de afstand tussen je ogen tot de totale breedte van je gezicht. Misschien verklaart het aantal Gulden Sneden die in het gezicht voorkomen, of iemand knap is of niet. Er is veel onderzoek gedaan naar gezichtsverhoudingen en aantrekkelijkheid, maar elk onderzoek heeft andere resultaten: onomstotelijk bewijs dat een Gulden Snede gezicht beter is, is er dus niet.

In de filosofie en religie
De Gulden Snede zie je in de natuur, muziek, schilderkunst en zelfs de menselijke schoonheid. Hoe kan het dat zo’n vreemd getal, bij benadering 1,62, zo een grote rol speelt? Daarover hebben wiskundigen, filosofen en kunstenaars lange tijd hun hoofd gebroken.
In de Middeleeuwen en Renaissance was het een godsbewijs: dat zonnebloemen, mensen en muziek voldeden aan één en dezelfde regel, dat moest haast wel komen doordat god alles schiep met een vooropgezet plan. Zelfs nu gebruiken sommige creationisten – die evolutie afwijzen als verklaring voor het ontstaan van leven en de ontwikkeling van soorten – het argument nog.
1 Leonardo van Pisa (ca. 1170 – ca. 1250), beter bekend onder zijn bijnaam Fibonacci, was een Italiaanse wiskundige. Hij wordt vaak beschouwd als de eerste westerse wiskundige die origineel werk publiceerde sinds de Griekse oudheid. Zijn Liber Abaci (uit 1202: Boek van het telraam) introduceerde het Arabische cijferstelsel in Europa (waar toen nog het Romeinse cijferstelsel gangbaar was). Het boek was vijfhonderd jaar toonaangevend. Het succes had ook te maken met de praktische toepassingsmogelijkheden die Fibonacci erin had opgenomen; zoals: methoden voor winst-en-verliesrekeningen, berekeningen voor rente-tarieven en tabellen voor wisselkoersen.
Het is niet duidelijk wie als eerste de rij heeft uitgedacht. De rij van Fibonacci wordt al genoemd in de Chhandah-shāstra, Kunst van het metrum, van de Sanskriet schrijver Pingala, omstreeks 450 v. Chr. of volgens andere datering omstreeks 200 v. Chr., onder de naam maatraameru. Uitvoeriger behandelden in de 6e eeuw Virahanka en later Acharya Hemachandra (1089–1172) de rij, om rekentechnisch het metrum te beschrijven door de regelmatige verdeling in korte en lange lettergrepen.
Toen Fibonacci 20 jaar was, ging hij naar Algerije waar hij Indiase en Arabische wiskunde bestudeerde en wellicht leerde hij daar de rij kennen. Hij was in het westen de eerste die de rij in zijn Liber abaci, noemde, bij het ‘konijnenprobleem‘.

