Archimedes, cilinder en kegel

De methode die Archimedes gebruikte om de verhouding te vinden tussen de inhoud van een cilinder en een ingeschreven kegel is een mooi voorbeeld van zijn geniale combinatie van geometrisch inzicht en vroege meetkundige integratie.

Archimedes en de verhouding tussen cilinder en kegel

Archimedes (287–212 v.Chr.) geldt als een van de grootste wiskundigen en natuurfilosofen uit de oudheid. Zijn werk over meetkunde is een hoogtepunt in de geschiedenis van de wiskunde, en zijn methoden worden nog altijd bewonderd vanwege hun elegantie.
Een van zijn klassieke resultaten betreft de verhouding tussen de inhoud van een cilinder en die van een ingeschreven kegel.

Het probleem

Neem een rechte cilinder en plaats daarin een rechte cirkelkegel waarvan:

de basis samenvalt met de basis van de cilinder
de top (het hoogste punt) samenvalt met het midden van de bovenste cirkelschijf van de cilinder.

De vraag die Archimedes zichzelf stelde was: Hoe verhoudt de inhoud van de kegel zich tot die van de cilinder?

De methode van Archimedes

Archimedes gebruikte geen algebra zoals wij dat doen. In plaats daarvan redeneerde hij geometrisch, vaak met behulp van zijn methode van uitputting – een voorloper van integraalrekening. Met die manier bereikte hij ook een prima benadering voor de waarde van π: 22/7.

Stel de figuren voor

Archimedes zag de cilinder als een figuur met het grondvlak een cirkel met straal r, en hoogte h.

Inhoud cilinder = oppervlak grondvlak × hoogte

De kegel heeft dezelfde cirkel met straal r als grondvlak en dezelfde hoogte h.

Methode van uitputting

Archimedes verdeelde de hoogte van zowel de cilinder als de kegel in een groot aantal dunne schijfjes (denk aan plakjes). Hij vergeleek de oppervlakten van die plakjes op dezelfde hoogte.

Voor de cilinder is elke schijf op hoogte z (gemeten vanaf de top) een cirkel met straal r, dus oppervlak:

A_cilinder(z)=πr²

Voor de kegel neemt de straal lineair af van r bij de basis (z=h) tot 0 (z=0) bij de top:

r(z)=rz/h

Dus het oppervlak op hoogte z is:

A_kegel(z)=π(rzh)²=πr²z²/h²

Integratie avant la lettre

Archimedes wist nog niet van integralen, maar hij gebruikte wel het idee dat de inhoud de som is van alle schijfoppervlakten (de methode van uitputting):

Volume Cilinder:

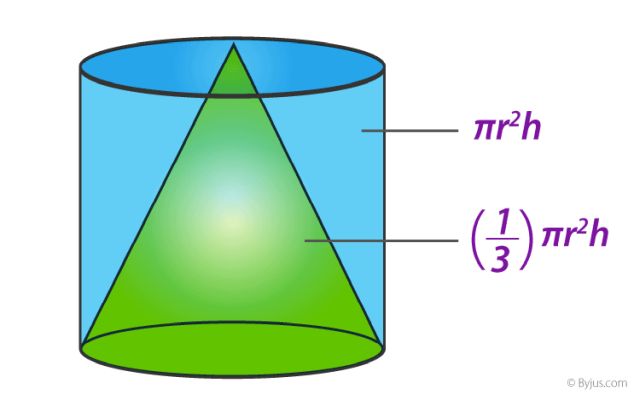
V_cilinder=πr²h

Volume Kegel (door vergelijking van verhoudingen van de schijfjes en meetkundige afleiding):

V_kegel=1/3πr²h

Hoe kwam hij aan die 1/3?

Archimedes gebruikte natuurlijk geen integralen, maar :

Hij vergeleek de volumes van deze figuren met bekende figuren (zoals prisma’s en piramides) waarvan de inhoud al exact bepaald was door de oude Egyptenaren en Grieken.
Hij bewees dat als je de hoogte van de kegel in n gelijke lagen verdeelt, de som van de volumes van die dunne schijfjes altijd dichter in de buurt komt van de werkelijke inhoud.
Door te redeneren dat bij n→∞ de benadering exact wordt, kon hij aantonen dat de inhoud van een ingeschreven kegel exact 1/3 van de cilinder is.

Het probleem van de kegel en cilinder toonde aan dat je met puur meetkundige redeneringen en zonder algebra nauwkeurige en universele formules kunt vinden. Archimedes wordt vaak gezien als een van de eerste denkers die een proto-vorm van integraalrekening gebruikte, bijna 2000 jaar voordat Newton en Leibniz de formele calculus ontwikkelden.
Zijn aanpak was ingenieus en berustte op twee pijlers: de methode van uitputting en mechanische analogieën.

De methode van uitputting

Deze techniek, die hij overnam en verfijnde van Eudoxus van Cnidus¹, bestond uit het benaderen van een kromlijnige figuur (zoals een cirkel, bol of paraboolsegment) door een reeks steeds kleinere meetkundige figuren waarvan de oppervlakte of inhoud wél exact berekend kon worden.

Hij verdeelde het te berekenen figuur in eenvoudige vormen (driehoeken, prisma’s, piramides).
Hij gebruikte limietdenken avant la lettre: door steeds meer figuren te gebruiken, wordt het verschil tussen de benadering en de echte waarde kleiner.
Wanneer het verschil kleiner werd dan een willekeurig klein getal, kon hij logischerwijs concluderen dat de benadering gelijk moest zijn aan de werkelijke waarde.

Voorbeeld:
Bij de inhoud van een kegel of bol verdeelde hij de hoogte in veel dunne lagen (schijfjes) en toonde aan dat de som van deze lagen exact de inhoud gaf.

Mechanische analogieën (De Methode)

In het in 1906 teruggevonden werk De Methode (gevonden in het beroemde Archimedes Palimpsest²) beschreef hij een verrassende aanpak: hij stelde zich voor dat de doorsneden van figuren mechanisch in evenwicht konden worden gebracht op een denkbeeldige balans.

Hij vergeleek de oppervlakten van doorsneden van onbekende lichamen met die van bekende lichamen.
Door de hefboomwet van Archimedes toe te passen (moment = kracht × arm), kon hij bepalen hoe de volumes zich tot elkaar verhielden.
Pas daarna gaf hij een formeel meetkundig bewijs, omdat zijn Griekse tijdgenoten een puur mechanisch redeneren niet als “strikt bewijs” zagen.

Betekenis voor Archimedes

Voor Archimedes was deze verhouding niet zomaar een rekenkundig weetje. Hij zag het als onderdeel van een groter geheel van ruimtelijke verhoudingen. In andere werken liet hij zien dat de inhoud van een bol precies twee derde is van die van de cilinder die hem omschrijft – een resultaat waar hij zelf het meest trots op was. Hij liet deze figuren zelfs graveren op zijn grafsteen.

¹ Eudoxus van Cnidus (410- 355 v.Chr.) was als leerling van Plato een veelzijdige wetenschapper, die uitblonk in wiskunde, geografie en astronomie. Al zijn werken zijn in de loop der tijden verloren gegaan. Wat we over hem weten, komt uit secundaire bronnen, uit de werken van Archimedes en bijvoorbeeld uit het gedicht over astronomie van de Hellenistische dichter Aratus.
Eudoxus was volgens de overlevering van arme afkomst, maar kon toch een behoorlijke opleiding genieten. Hij was afkomstig van het Ionische eiland Cnidus, en leefde jaren in Athene waar hij onder andere les in wiskunde kreeg van Archytas van Tarente.
Hij heeft ook een reis ondernomen naar Egypte waar hij enkele jaren bleef.

In de wiskunde was hij de voorloper van Euclides en heeft hij verschillende axioma’s opgesteld. Euclides heeft heel wat bewijzen van Eudoxus overgenomen en mogelijk zelfs hele werken. Eudoxus’ belangstelling ging vooral uit naar onder andere de gulden snede, de doorsnede van krommen, het Delisch probleem (= verdubbeling van een kubus).

Eudoxus is degene die als eerste de uitputtingsmethode nauwkeurig heeft beschreven, een manier om het binnen-oppervlak van een gekromde figuur, zoals een cirkel te bepalen. Deze uitputtingsmethode ligt aan de basis van de integraalrekening.

² De Archimedespalimpsest is een palimpsest, een hergebruikt perkament, uit de 13e eeuw waarin een tekst van Archimedes is verborgen. Het document is van buitengewoon belang voor de geschiedenis van de wetenschap. Het werk bevat de enige overgeleverde Griekse versie van Drijvende lichamen en de enige afschriften van de Methode van mechanische stellingen en Stomachion.