Archimedes stuurde zijn geometrische vindingen naar minstens drie geleerden in Alexandrië – Conon, Dositheus en Eratosthenes.
Conon was een wiskundige en astronoom die Archimedes waardeerde als een vriend. Nadat Conon stierf, begon Archimedes te corresponderen met Dositheus. Archimedes schreef dat Dositheus ‘bedreven was in meetkunde‘, maar verder is er weinig bekend over de man die de originele kopieën van zoveel van Archimedes’ ontdekkingen als eerste ontving.
Eratosthenes, de derde geleerde die correspondeerde met Archimedes, blijft beroemd om zijn vele
opmerkelijke prestaties. Eratosthenes was een wiskundige, geograaf en astronoom.
Hij diende als hoofdbibliothecaris in Alexandrië en schreef boeken over geografie, theater en wiskunde.
Tweeëntwintig eeuwen geleden heeft Eratosthenes de omtrek gemeten van de aarde met verbazingwekkende nauwkeurigheid1. De oude Grieken wisten al dat de aarde een bol was (hey, flatearthers!). Voor zijn berekeningen maakte Eratosthenes gebruik van schaduwen die werden geworpen als de zon het hoogste punt aan de hemel stond.
Eratosthenes berekende ook de afstand van de aarde tot de zon, bracht de bekende wereld in kaart en ontwikkelde een kalender met schrikkeljaren.
Eratosthenes, Conon en Dositheus waren alle wiskundigen die de ontdekkingen (en de bijbehorende redeneringen) van Archimedes konden begrijpen. Behalve dat zij er zelf wijzer van werden, konden zij de kennis ook doorgeven aan hun leerlingen.
Meetkunde
Archimedes schreef meer over meetkunde dan over welk ander onderwerp. Veel van zijn boeken zijn ontdekkingen over cirkels, spiralen, bollen en andere figuren begrensd door gebogen lijnen en vlakken. “Meting van een Cirkel”, “Over de Bol en Cilinder”, “Over Spiralen” en “Kwadratuur van de Parabool” zijn de titels van enkele van Archimedes’ boeken die te maken hebben met gebogen figuren.
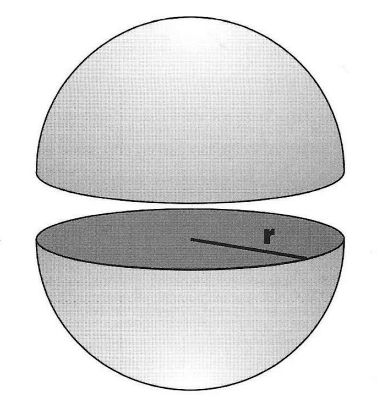
Bol
“Het oppervlak van elke bol”, schreef Archimedes, “is gelijk aan vier keer dat van zijn grootste cirkel.”
Cilinder
“Elke cilinder waarvan de basis gelijk is aan de grootste cirkel in de bol en van wie hoogte is gelijk aan de diameter, is zelf half zo groot als weer de bol en het oppervlak is half weer zo groot als het oppervlak van de bol,” schreef Archimedes.
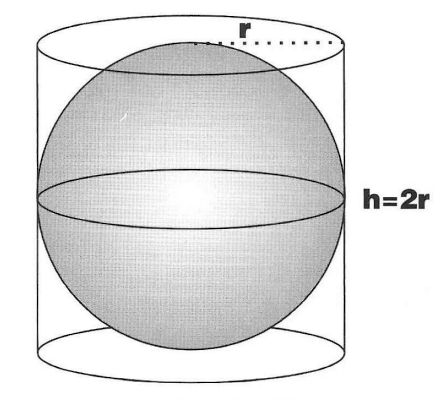
Als de diameter van de bol en cilinder hetzelfde zijn, dan is het volume van de bol precies tweederde van het volume van de cilinder. Een andere manier om dit te zeggen is dat het volume van de cilinder drie helften van het volume van de bol is.
Archimedes ontdekte dat dezelfde relatie bestaat tussen de oppervlakte van de bol en cilinder. Met andere woorden, het gebogen oppervlak van de bol is precies tweederde zo groot als het oppervlak van de cilinder.
Je vraagt je toch af hoe hij dat gedaan heeft zonder de huidige wiskundige kennis over het berekenen van oppervlakten met integralen.
1 Hoe deed Eratosthenes dat? Hem viel de hoek van de schaduw op die de zon op een bepaalde dag in Alexandrië werpt… wetende dat in een put honderden kilometers verderop een stok die dag op het middaguur geen schaduw wierp, vanwege de hoek van de zon.
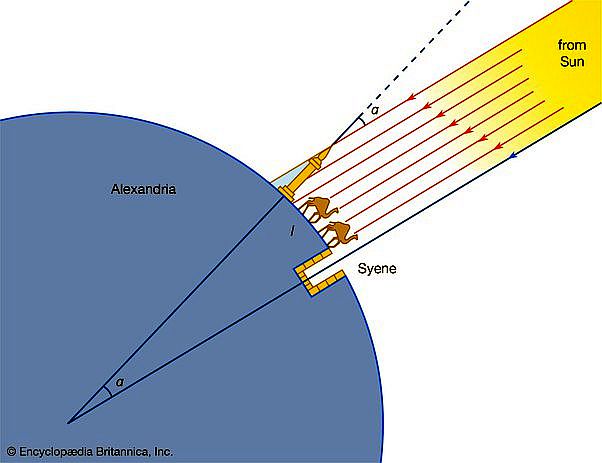
Door een trigonometrie toe te passen, bepaalde hij hoeveel een boog op een cirkel deze twee punten scheidde. Vervolgens berekende hij de grootte van de aarde met zeer grote nauwkeurigheid.

