In de notatie maand/dag van de datum 14 maart, kom je op de eerste cijfers van Pi: 3,14.
Het geeft de verhouding tussen de omtrek en de diameter van een cirkel. Maar vreemd genoeg komt Pi op veel meer plekken in de wis- en natuurkunde te voorschijn, terwijl daar helemaal geen cirkels in beeld zijn! Zoals in de kosmologie, thermodynamica, elektromagnetisme en statistiek.
Door deze alomtegenwoordigheid is π zelfs bekend bij mensen die niets moeten weten van wiskunde en daardoor ook doorgedrongen in de internet- en populaire cultuur.
Irrationeel
Pi is een irrationaal getal, en dat betekent dat het niet als een breuk te schrijven is. En dat betekent weer dat er een oneindig aantal decimalen nodig zijn om de juiste waarde te benaderen (en dan ook nog een oneindige reeks zonder repetitieve gedeelten).
Al duizenden jaren wordt er geprobeerd om vat te krijgen op Pi (π).
De Griekse wiskundige Archimedes gaf rond 250 v. Chr. met 22/7 een opmerkelijk nauwkeurige benadering van π.
Transcendent
Een deel van de irrationale getallen is transcendent en ook π blijkt dat te zijn. Dit betekent dat het getal niet is te schrijven als oplossing van een algebraïsche vergelijking met een eindig aantal termen.
Daaruit volgt tevens dat er geen constructie met passer en liniaal bestaat om een rechte lijn te construeren die lengte π heeft. Heel anders dan een getal als √2, dat wel irrationaal maar niet transcendent is, en daarom wel geconstrueerd kan worden: de schuine zijde van een eenvoudig te construeren gelijkbenige rechthoekige driehoek met rechte zijde 1 heeft de lengte √2.
Met π is iets dergelijks onmogelijk.
Dit doet me denken aan een gedachtenexperiment dat ik op de middelbare school had: de oppervlakte van een cirkel zou je kunnen benaderen door de oppervlaktes te berekenen van het ingeschreven en omschreven vierkant. Ik bedoel het volgende:
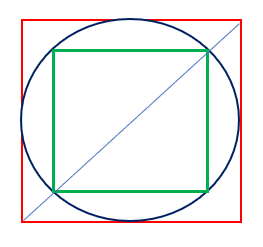
De oppervlakte van het rode vierkant om de cirkel is groter dan het oppervlak van de cirkel. En zo is dat van het groene vierkant in de cirkel kleiner. Het oppervlak van de cirkel lijkt er tussen in te zitten.
Als de cirkel straal r heeft, dan is met behulp van de stelling van Pythagoras de zijde a van het groene vierkant in r uit te drukken (het deel van de blauwe lijn binnen het groene vierkant is 2x de straal r van de cirkel): a2 + a2 = (2r)2 ofwel 2a2 = 4r2 en dat betekent weer dat het oppervlak van het groene vierkant (a2) = 2r2.
Beredeneer zelf dat de oppervlakte van het rode vierkant gelijk is aan : 2 * 2r * r = 4r2 .
Dus de oppervlakte van de cirkel ligt tussen 2r2 en 4r2 ! In werkelijkheid πr2 , dus π ligt tussen 2 en 4.

