Ramsey theorie en de complotten

Onlangs las ik ergens dat de basis van alle complottheorien een redelijk simpele wiskundige theorie is.
Die theorie is vernoemd naar de Britse wiskundige Frank Ramsey (1903-1930).
In 1926 werd Ramsey universitair docent in de wiskunde en later directeur wiskundige studies aan King’s College. Toen Wittgenstein zijn Tractatus Logico-Philosophicus als doctoraal proefschrift in Cambridge verdedigde, was Ramsey Wittgensteins promotor.

De theorie gaat over de vraag hoeveel elementen uit een met een zekere wiskundige structuur uitgeruste verzameling gekozen moeten worden, opdat dezelfde wiskundige structuur in een deelverzameling teruggevonden kan worden, waarbij tevens aan een bepaalde eigenschap wordt voldaan.

Ballen in Postvak

Dat is misschien niet meteen helder, maar dat wordt het met het zogenaamde postvak voorbeeld:

Stel je hebt 5 postvakken en 6 ballen, dan is er, bij de verdeling van alle ballen over de postvakken, minstens één vak met 2 ballen; dat voelt iedereen wel met zijn klompen aan.

We kunnen dit wat algemener maken: er komen ten minste 2 ballen in één bak bij het verdelen van n ballen over (n – 1) bakken (met n > 1).

En dan nog een stap verder: er is een bak met ten minste a ballen, na het verdelen van n(a – 1) + 1 ballen aan n bakken (weer met n > 0 , a > 0 ).

Complottheorie

Maar wat heeft dit met complottheorien te maken?

Het postvakprincipe laat zien dat een willekeurige structuur (in dit geval een willekeurige verdeling van ballen over een vast aantal bakken) vanaf een bepaalde omvang (een bepaald aantal ballen) noodzakelijkerwijs een regelmatige deelstructuur moet bevatten (een bak met minimaal een bepaald aantal ballen).
De minimale omvang waarbij een regelmatige deelstructuur noodzakelijkerwijs optreedt kan in sommige gevallen (zoals in het geval van het postvakprincipe) exact berekend worden.

Kortgezegd komt het erop neer dat totale chaos onmogelijk is: vanaf een bepaalde omvang moeten willekeurige structuren noodzakelijkerwijs regelmatige deelstructuren bevatten.

Dus als we alle letters van de Statenvertaling van de Bijbel (dat is een voldoende aantal elementen) in een bepaalde tabelstructuur zetten (willekeurige structuur), zal er ongetwijfeld ergens een zinsnede staan die het einde van de wereld voorspelt (de regelmatige deelstructuur).

Bewijs van de Ramsey theorie

Wiskundige Ann Dooms (VUB) legt de ‘Ramseytheorie‘ uit aan de hand van zes willekeurige Facebook-profielen.

“Het idee valt het eenvoudigst te illustreren in termen van netwerken, zoals de sociale netwerken die je op Facebook vindt. Kies zes willekeurige personen op Facebook. Deze individuen kunnen bij voorbaat al onderling bevriend zijn of niet. Hoe dan ook: je hebt altijd ofwel een groepje van minstens drie personen die onderling bevriend zijn, ofwel een groepje van minstens drie personen die geen vrienden zijn.”

Laten we die zes profielen opvatten als punten in een graaf¹. Als twee mensen vrienden van elkaar zijn, geven we dat aan met een rode lijn tussen de corresponderende punten. Als twee mensen geen vrienden van elkaar zijn, geven we dat aan met een blauwe lijn tussen de punten.
In deze context wordt Ramsey’s theorie: als je in een graaf van zes punten, waarbij alle punten met elkaar verbonden zijn, alle lijnstukken wilt kleuren met de kleuren rood en blauw, dan is er altijd een rode driehoek of een blauwe driehoek. Dit kunnen we wel bewijzen.

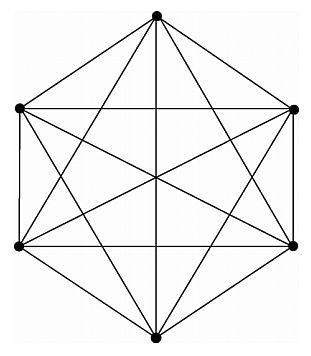
Kies een willekeurig punt in de graaf en noem dit V. In dit punt komen vijf lijnstukken samen. Dit geldt namelijk voor alle punten in de graaf. Er zijn nu minstens drie van deze lijnstukken met dezelfde kleur. Er zijn namelijk vijf lijnen en twee kleuren, dus er zijn minstens drie lijnen met dezelfde kleur.
We nemen nu even aan dat deze kleur rood is. Dit kunnen we zeker aannemen, omdat we de kleuren altijd nog kunnen verwisselen. Noem de punten aan het einde van de drie lijnstukken A, B en C.

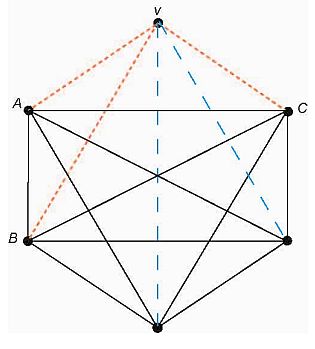
We bekijken nu de lijnstukken tussen de punten A, B en C. Er zijn nu twee mogelijkheden:

1. De lijnstukken tussen deze punten zijn allemaal blauw, dan vormt ∆ ABC een blauwe driehoek.
2. Een lijnstuk tussen AB, BC of CA is rood dan vormt een van de driehoeken: ∆ ABV, ∆ BCV of ∆ CAV een rode driehoek.

En dat wilden we bewijzen, QED.

In deze willekeurige selectie van zes profielen hebben we structuur gevonden: een groepje vrienden, of een groepje vreemden. Als we slechts vijf personen hadden gekozen, had dit fenomeen zich niet voorgedaan.
Het achterliggende idee is dat zolang het netwerk groot genoeg is er altijd structuur zal opduiken. Dat hoeven niet altijd vrienden of vreemden te zijn. Het kan ook gaan om andere, complexere structuren.

Implicaties van Ramsey’s theorie

De theorie heeft verregaande implicaties. In het voorbeeld met Facebook lijkt het logisch om op zoek te gaan naar grotere groepen vrienden of vreemden. Hoeveel profielen moeten we bijvoorbeeld kiezen om gegarandeerd een groepje van vier vrienden of vier vreemden aan te treffen? En wat als we dat voor eender welke grootte n zouden willen weten? Dat is exact hoe het Ramseygetal R(n) kan worden gedefinieerd. Het is het minimale aantal profielen dat we moeten kiezen om zeker een groep van n vrienden of n vreemden te vinden.

Ramseygetal

Zoals we in het Facebook voorbeeld hebben gezien is R(3) = 6. Met wat meer werk kun je aantonen dat R(4) = 18. Vanaf n = 5 wordt het al een heel ander verhaal, want tot op de dag van vandaag is de precieze waarde van R(5) onbekend. Om een idee te geven: in 1997 konden experts aantonen dat R(5) ≤ 49. Pas twintig jaar later kon men bewijzen dat R(5) ≤ 48. Omgekeerd weten we dat 43 ≤ R(5), en sommige experts zijn ervan overtuigd dat inderdaad R(5) = 43. Aan het huidige tempo van bewijzen kunnen we een sluitend bewijs pas verwachten in het jaar 2117.

Atomen in het Universum

De wetenschappelijke vooruitgang en rekenkracht van computers gaan natuurlijk steeds sneller, dus waarschijnlijk komt er nog deze eeuw een oplossing voor R(5). Al is dat minder waarschijnlijk dan je zou denken. Als je met brute kracht wil aantonen dat R(5) ≤ 43, dan zou de computer zo’n 10²⁸⁴ gevallen moeten doorlopen. Dat is een hoeveelheid waarbij het aantal atomen in het universum in het niet valt.

Verdere generalisatie

Ramsey heeft deze stelling nog veel verder gegeneraliseerd. Je kunt je bijvoorbeeld afvragen hoe groot de groep mensen moet zijn zodat je altijd vier vrienden of niet-vrienden hebt. Dit getal wordt ook wel R(4,4) genoemd. Het blijkt dat zelfs de slimste wiskundigen het bij vijf al niet meer weten.
Eén van de grote wetenschappers binnen de grafentheorie, de Hongaar Paul Erdös, zei zelfs eens: “Imagine an alien force, vastly more powerful than us, landing on Earth and demanding the value of R(5, 5) or they will destroy our planet. In that case, we should marshal all our computers and all our mathematicians and attempt to find the value.
But suppose, instead, that they asked for R(6, 6), our only option is an attempt to destroy the aliens”.

Frank Ramsey: A sheer excess of powers

Over het leven van Frank Ramsey is een biografie verschenen: Frank Ramsey. A sheer excess of powers door Cheryl Misak. Daarin wordt duidelijk dat werk en leven van Ramsey innig verbonden waren.

Ramsey zou maar 26 worden, ten gevolge van een leveraandoening. In het boek wordt duidelijk hoe een bijzonder mens, en hoe een fantastische geest, Frank Ramsey was. Helaas is hij (nog) niet zo bekend bij het grote publiek.

Jeugdjaren

Hij werd geboren in een gezin vol tegenpolen. Moeder Agnes was politiek zeer betrokken, zette zich in voor progressieve doelen zoals vrouwenkiesrecht. Vader Arthur daarentegen was stil, streng, misschien wel een beetje saai, en kon soms plots in woede uitbarsten. Frank was een overtuigd atheïst, zijn broertje Michael zou later aartsbisschop van Canterbury worden, de hoogste positie in de Anglicaanse kerk. Frank leek meer op zijn moeder dan zijn vader, en ondanks dat zijn familie uit een gegoed milieu kwam – upper-middle class, zoals de Britten zeggen – zou Ramsey altijd het belang van de kansarme klassen voorop stellen.

Het kille Winchester College

Al tijdens zijn vroege jongensjaren op het vreselijke Winchester College zou Ramsey blijk geven van een groot talent. Ondanks de dagelijkse koude baden, het zeer slechte eten en pestgedrag van oudere jongens toonde hij al vroeg een groot talent in de wiskundeles. Zijn docent klassieke talen was aanvankelijk minder onder de indruk. Toen vader Arthur naar school kwam zei de docent dat hij nog niet erg ver gevorderd was. ‘Hoe gevorderd verwacht je dat een twaalfjarig jongetje kan zijn?’ vroeg Arthur. ‘Mijn hemel, is hij pas twaalf? Ik dacht dat hij vijftien was’, antwoordde de docent.
Het zegt veel over Franks talent, hoewel zijn uitzonderlijke lengte vast ook bijdroeg aan het misverstand. Ook toonde hij toen al een sterke interesse voor politiek, hoewel hij zich nooit aan één bepaalde stroming vastlegde. Hij debatteerde veel met klasgenoten over rechtvaardigheid, kapitalisme, socialisme en privaat bezit, wellicht aangewakkerd door de politieke onrust aan het einde van de Eerste Wereldoorlog, die ook in Winchester College zeer voelbaar was geweest.

Tegelijk verorberde hij boeken alsof het koekjes waren. Hij las Marx, Keynes, Weyl, Mach, Kant, Hume en Russell. Dit nog allemaal voor hij naar de universiteit ging, op zijn zestiende.

Het bruisende Cambridge

Hij ging naar Cambridge, waar zijn vader ook als wiskundeleraar werkte. Op dat moment zoemde het in Cambridge van de activiteit en de nieuwe ideeën. Op de filosofiefaculteit maakten Russell en Moore de dienst uit, Wittgenstein was net naar Duitsland vertrokken om les te geven aan schoolkinderen. Wiskunde werd gedomineerd door Littlewood en Hardy. Economie werd een minder speculatieve en meer wetenschappelijke discipline dankzij het werk van Keynes en Pigou en (later) Sraffa.

Ook het culturele leven in Cambridge was zeer vruchtbaar. In discussiegroepen met bijna mystiek aandoende namen als de Heretics en de Apostles verkeerden intellectuelen als Keynes, Russell, Moore, Leonard Woolf, Lytton Strachey en E.M. Forster. Ze bespraken de Freudiaanse psychoanalyse, zeer modieus in die tijd, en hielden er een vrije seksuele moraal op na, waarin homoseksuele clubgenoten openlijk zichzelf konden zijn.

Ramsey maakte op bijna iedereen die hij ontmoette een grote indruk. Niet alleen vanwege zijn grote, gulle lach en zijn enorme postuur, maar ook vanwege zijn scherpe geest en zijn gave om slechte ideeën vlijmscherp te fileren. (Het is veelzeggend dat Moore, een van de belangrijkste filosofen in zijn tijd, nerveus werd als Ramsey in de collegebanken zat.)

Geen dogmatische socialist

In het boek schetst Misak Ramseys intensieve en productieve jaren in de gloriedagen van Cambridge in schitterende kleuren. Bijna iedereen die terloops ter sprake komt wordt wel minister-president, gelauwerd kunstenaar of eminent academicus. De eerste paar hoofdstukken, van zijn geboorte tot zijn benoeming als university lecturer in de wiskunde aan King’s College in 1926 (hij is dan 23!) zijn daarom het interessantst. Waar Misak ook heel goed in slaagt is te laten zien dat Ramseys persoonlijkheid wel degelijk zijn werk beïnvloedt en andersom.
Ramsey was een overtuigd socialist, hoewel hij nooit dogmatisch werd, en ook in zijn werk streefde hij naar kansen-gelijkheid. Als econoom hield hij zich bijvoorbeeld bezig met eerlijke belastingen en de vraag hoeveel de overheid moest sparen. Hij ging er niet van uit dat mensen perfect rationeel waren en precies wisten hoe ze hun koopkracht moesten vermeerderen, zoals sommige collega-economen wel plachten te doen.

Geen dogmatische filosoof

Ook als filosoof was Ramsey nooit dogmatisch. Hij liet zich niet meesleuren in de traditie van Russell, Moore en (de vroege) Wittgenstein. Die zagen voor de wiskunde en de logica een bijzonder grote rol weggelegd binnen de filosofie.
Als je de logica goed toepaste kon je er filosofische problemen mee oplossen, dachten zij, want die kwamen voort uit de manier waarop we de taal gebruiken. Het was een populair idee dat de betekenis van woorden lag in de objecten waar ze naar refereerden. ‘Frankrijk’ refereert naar Frankrijk; ‘boek’ refereert naar een boek. Maar met sommige zinnen doen zich problemen voor: In ‘De koning van Frankrijk is kaal’ refereert ‘De koning van Frankrijk’ nergens naar, want Frankrijk heeft geen koning. Is de zin nu onwaar? Of nonsens?
Ramsey dacht, grof gezegd, dat zijn voorgangers tegen windmolens vochten. Je kunt taal wel héél precies maken met logica, maar dan houd je iets over wat geen taal meer is, maar wiskunde. Ramsey had een meer pragmatische houding. Niet dat hij zich er gemakkelijk vanaf maakte, maar hij vond wel dat een theorie zich bewees door hoe nuttig en waardevol die in praktijk bleek te zijn. Voor hem ligt de betekenis van ‘De koning van Frankrijk is kaal’ in hoe de zin gebruikt wordt, welk gedrag het uitlokt, en dergelijke.

Wel pragmatisch

Naast zijn pragmatische insteek dichtte Ramsey ook de psychologie een grote rol toe, onder invloed van zijn gesprekken over Freud bij de Heretics en de Apostles, en zijn eigen ervaringen met de psychoanalyse. Hij ging een jaar naar Wenen om daar geanalyseerd te worden.

Hoe kunnen we erachter komen welke zinnen waar zijn en welke niet? Russell had daar een heel logisch systeem voor gebouwd, waarbij we kijken naar waar woorden naar refereren in de echte wereld. Ramseys oplossing was veel psychologischer: kijk naar hoe iemand zich gedraagt. Als je de uitspraak ‘het regent’ voor waar houdt, zul je niet snel zonder paraplu naar buiten gaan. Daarmee verbond hij het begrip ‘waarheid’ aan overtuigingen en handelingen, een revolutionaire zet.

De mens op de voorgrond

Ramsey had een kort, maar gelukkig leven. Hij was gelukkig getrouwd en dol op zijn twee dochtertjes. Hij had stimulerend werk en veel vrienden. Toch is de biografie daarom niet saai. Misak heeft een vlotte pen en wordt nergens technisch. Voor de liefhebbers zijn er korte kaders, geschreven door experts, die bijvoorbeeld de wiskunde achter Ramseys economie uitleggen. Ze weet, met name in het begin, de wederzijdse invloed van Ramseys leven en werk goed duidelijk te maken. De tweede helft van het boek is iets taaier, omdat het daar vooral gaat over Ramseys ideeën.
Voor iemand zonder achtergrond in de filosofie of de economie staan in dat tweede deel best pittige paragrafen. Maar die kun je makkelijk overslaan en toch een idee krijgen van wat Ramsey heeft betekend voor de filosofie, de economie en de wiskunde. En dat is dat hij in alle drie die disciplines de aanzet heeft gegeven voor een omwenteling naar een psychologisch en een pragmatisch perspectief. En dat is wat de disciplines toen hard nodig hadden.

In een lezing aan de Cambridge Apostles somt hij zijn wereldbeeld mooi op: “Humanity, which fills the foreground of my picture, I find interesting and on the whole admirable. I find, just now at least, the world a pleasant and exciting place.”

¹ Een graaf is een verzameling van punten en verbindende lijnen daartussen.