Een brief, gedateerd 16 januari 1913, arriveerde op het bureau van professor Godfrey Harold Hardy, destijds professor aan de prestigieuze Universiteit van Cambridge, en luidde ongeveer zo:
“Geachte heer, ik wil mezelf graag voorstellen als griffier op de boekhoudafdeling van het Port Trust Office in Madras (India). Ik ben 23 jaar oud en heb geen universitaire opleiding genoten, maar sinds ik van school ben gegaan, besteed ik mijn vrije tijd aan wiskunde. Ik verzoek u de bijgevoegde papieren te onderzoeken. Als u ervan overtuigd bent dat er iets van waarde in zit, zou ik graag willen dat mijn stellingen gepubliceerd worden. Ik zou uw advies zeer op prijs stellen. Srinivasa Ramanujan.”
5000 Stellingen
Ramanujan, geboren in 1887 in Erode (India), sprak de eerste drie jaar van zijn leven nauwelijks een woord, zozeer zelfs dat zijn moeder vreesde dat hij stom was. Zijn wiskundige talent kwam al vroeg naar voren en op elfjarige leeftijd had hij de kennis van twee universiteitsstudenten die bij hem thuis logeerden al overtroffen.
Op zijn vijftiende leende hij een op zijn zachtst gezegd bizar boek, waarin ongeveer vijfduizend stellingen stonden, allemaal zonder bewijs. Ramanujan stelde zichzelf ten doel om zonder enige vorm van hulp alle formules in het boek af te leiden. In de praktijk had hij zichzelf een ‘onderzoeksproject’ opgezet over duizenden afzonderlijke onderwerpen. Hij was echter te arm om papier te betalen, dus voerde hij de berekeningen uit op een schoolbord en schreef de resultaten op in een reeks notitieboekjes, die tot op de dag van vandaag zijn grootste erfenis blijven, die hij zijn hele leven heeft bewaard.

Toen hij ziek werd, verscheen hij op een karretje bij het huis van een vriend en liet zich vergezellen door de dokter. Voordat hij naar binnen ging, zei hij tegen hem: “Als ik sterf, laat ze dan bij deze twee professoren bezorgen“, terwijl hij twee grote boeken vol wiskunde in zijn handen legde. In feite waren die notitieboekjes een soort introductiebrief voor zijn talent geworden, en hij liet ze aan iedereen zien om een baan te krijgen.
Naar Cambridge
Dankzij zijn koppigheid en een flinke dosis geluk slaagde hij erin contact op te nemen met professor Hardy, die onmiddellijk actie ondernam om hem naar Cambridge te brengen. Maar Ramanujan wilde India aanvankelijk niet verlaten. Via de Engelse Universiteit slaagde hij erin een plek te vinden aan de Universiteit van Madras en won hij een speciale beurs. Ondertussen drong Hardy aan om hem naar Groot-Brittannië te brengen, maar het grootste probleem werd zijn moeder, die pas overtuigd was nadat ze had gedroomd van de godin Namagiri1 die haar opdroeg de droom van haar zoon waar te maken.
In Engeland
Ramanujan arriveerde in april 1914 in Engeland. Hij werd volledig ondergedompeld in de wiskunde, werkte dag en nacht, waarna hij uitgeput instortte en twintig uur sliep. Zijn toch al slechte gezondheid ging langzaam achteruit en hij kreeg opnieuw een ziekte die niet werd gediagnosticeerd. Men dacht dat het een maagzweer was, daarna kanker en uiteindelijk werd hij behandeld voor tuberculose.
In de loop van twee jaar werd hij door acht artsen gezien en opgenomen in vijf verschillende ziekenhuizen. Uiteindelijk ontving hij academische onderscheidingen en werd hij de eerste Indiase Fellow van de Royal Society.
In het voorjaar van 1919 besloot hij terug te keren naar India. De lange reis verslechterde zijn gezondheid enorm en hij stierf slechts een jaar later.
Speciaal talent
Ramanujan redeneerde op een buitengewone manier. Hij was in staat om tot correcte resultaten te komen, maar met minder rigoureuze methoden. Hij zou zelf hebben gezegd dat de godin Namagiri hem de resultaten in zijn dromen vertelde. Hardy herinnerde zich hem als volgt:
“Zijn gave voor wiskunde viel niet te ontkennen. Hij had een diepgaande originaliteit en zou waarschijnlijk een grotere wiskundige zijn geweest als hij in zijn jeugd een beetje getemd was geweest. Aan de andere kant zou hij minder een Ramanujan en meer een Europese professor zijn geweest, en het verlies zou groter kunnen zijn geweest dan de winst.”
Wiskundige resultaten en prestaties
In de wiskunde bestaat een belangrijk onderscheid tussen het hebben van wiskundig inzicht en het leveren van een bewijs. Ramanujans talent lag duidelijk op het hebben van een gigantisch instinctief en intuïtief wiskundig inzicht, met een voorkeur voor de getaltheorie.
Ramanujan liet een grote hoeveelheid ongeordend materiaal na met vele originele stellingen. Vanwege zijn gebrek aan een formele wiskundige opleiding, gaf hij echter meestal geen bewijzen bij zijn stellingen Pas tussen 1985 en 1997 werden zijn aantekeningen geordend en bewezen door Bruce C. Berndt en zijn medewerkers. In totaal heeft hij zo’n 4.000 stellingen nagelaten.
Een bezoek van Hardy waaruit de begaafdheid van Ramanujan bleek:
Ik herinner me dat ik hem eens aan zijn ziekbed in Putney (Londen) bezocht. Ik was met taxi nr. 1729 gekomen. Het getal kwam mij tamelijk saai voor en ik merkte op dat ik hoopte dat het geen ongunstig voorteken was. ‘Nee’ was het antwoord van Ramanujan, ‘het is een zeer interessant getal. Het is het kleinste getal dat op twee verschillende manieren als de som van twee derdemachten kan worden uitgedrukt.’
Taxicab numbers
Sindsdien worden in de getaltheorie de kleinste getallen die op n verschillende manieren als de som van twee derdemachten kunnen worden geschreven taxicab numbers genoemd.
Ramanujans klaarblijkelijk talent voor diepe inzichten leverde een overvloed aan formules op, die vervolgens later in diepte konden worden onderzocht. Er wordt gezegd dat Ramanujans ontdekkingen buitengewoon rijk zijn en dat er vaak veel meer in zit dan op het eerste gezicht lijkt.
Manieren om Pi te berekenen
Als een bijproduct van zijn inzichten hebben zich zelfs een aantal nieuwe onderzoeksrichtingen in de wiskunde geopend. Onder de voorbeelden van de interessantste van deze formules zijn de intrigerende oneindige rijen voor π, een waarvan hieronder wordt gegeven:

Ramanujan-rijen voor π convergeren buitengewoon snel (exponentieel) en vormen de basis van sommige van de snelste algoritmen die momenteel worden gebruikt om π te berekenen. Afbreken van de som van de eerste term geeft ook een benadering

voor π, die tot op zes decimalen correct is.
Kettingbreuk
Een van zijn opmerkelijke vermogens was het snel oplossen van problemen. Hij deelde een kamer met P.C. Mahalanobis die een probleem had,
“Stel je voor dat je op een straat loopt met huizen die van 1 tot en met n genummerd zijn. Er is ergens een huis (x) zodanig dat de som van de huisnummers links van huis x gelijk is aan de som van de huisnummers aan de rechterkant van huis x. Als n tussen 50 en 500 ligt, wat zijn de waarden voor n en x. ”
Dit is een bivariaat probleem met meerdere oplossingen. Ramanujan dacht hier even over na en gaf een verrassend antwoord: hij gaf een kettingbreuk. Het ongebruikelijke hiervan was dat deze kettingbreuk de oplossing was voor de hele klasse van dergelijke problemen.
Mahalanobis was verbaasd en vroeg hoe hij dit antwoord had gevonden. “Het is eenvoudig; het moment dat ik over het probleem hoorde wist ik dat het antwoord een kettingbreuk was.“
Partitie-functie, Ramanujan-functie en de supersnaartheorie
In 1918 bestudeerden Hardy en Ramanujan de partitiefunctie P(n)1 uitvoerig. Zij gaven een niet-convergente asymptotische reeks die een exacte berekening van het aantal partities van een geheel getal mogelijk maakt. Hans Rademacher was in 1937 in staat deze formule te verfijnen en zo een exacte convergente reeksoplossing voor dit probleem te vinden.
Het werk van Ramanujan en Hardy op dit gebied heeft geleid tot een krachtige nieuwe methode voor het vinden van asymptotische formules, die de cirkelmethode wordt genoemd.
De naar hem genoemde Ramanujan-functie is tegenwoordig van belang in de supersnaartheorie. Deze functie verklaart waarom er, als de supersnaartheorie waar is, 10 of 26 dimensies moeten zijn.
1 Namagiri: De grote Indiase wiskundige Srinivasa Ramanujan schreef zijn wiskundige bevindingen toe aan Namagiri Thayar, de godin van zijn familie. Volgens Ramanujan verscheen ze aan hem in visioenen en stelde ze wiskundige formules voor die hij vervolgens zou moeten verifiëren. Eén zo’n gebeurtenis werd door hem als volgt beschreven: ‘Terwijl ik sliep, had ik een ongewone ervaring. Er was als het ware een rood scherm gevormd door stromend bloed. Ik observeerde het. Plotseling begon een hand op het scherm te schrijven, dat trok alle aandacht. Die hand schreef een aantal elliptische integralen. Ze bleven in mijn gedachten hangen.’ Bovendien kreeg de moeder van Ramanujan toestemming van Namagiri Tayar om Ramanujan naar Engeland te laten gaan.
| 2 Uit hoeveel sommen is de uitkomst 20? (Uitleg van de Partitie-functie door Hofstede) De oplossing is snel te zien, als je het getal 20 ziet als een ketting van 20 enen. Een optelsom fabriceren komt dan neer op het doorknippen van de ketting op verschillende plaatsen. Hieronder is bijvoorbeeld de som 20 = 6 + 2 + 7 + 5 gefabriceerd. 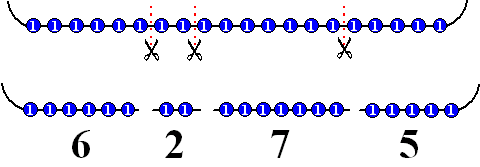 Dus het aantal sommen waar 20 uit komt is gelijk aan het aantal manieren waarop we de 20-ketting in stukken kunnen knippen. Er zijn 19 mogelijke plaatsen waar we kunnen knippen. Bij elke plaats moeten we beslissen JA (knippen) of NEE (niet knippen). Dat kan dus op 219 manieren. Alleen de variant waar we NIETS doorknippen levert geen som op, want 20 zelf is geen som. Het aantal sommen is dus 219 – 1 oplossing: 219 – 1 = 524287 sommen |
| Maar goed, dit was een makkie, een veel interessantere vraag is natuurlijk: Hoeveel ECHT verschillende sommen zijn er waar 20 uit komt? Want wees nou eerlijk: 4 + 14 + 2 is natuurlijk hetzelfde als 2 + 4 + 14. Noem P(n) het aantal ECHT verschillende manieren (ofwel de Partitie functie). Bijvoorbeeld P(5) = 7, namelijk 5 , 4+1 , 3+2, 3+1+1 , 2+2+1 , 2+1+1+1 en 1+1+1+1+1 Dat aantal is echter in het algemeen niet zo simpel te berekenen! Goldbach schreef een brief aan Euler waarin hij hem vroeg naar de waarden van P(n). Creatief als altijd, produceerde Euler een methode om functies te genereren voor een antwoord op de vraag. |
