Op Quora vond ik deze interessante bijdrage van een mathematicus over het eenvoudigste wiskundeprobleem dat de meeste mensen niet kunnen oplossen, en waarom?
“Toen ik College Algebra gaf, legde ik, op een geschikt moment in de cursus, dit probleem aan de studenten voor:
Simpele som
Ik reed gisterochtend heel vroeg naar mijn werk – er was geen verkeer en mijn gemiddelde snelheid was 40 mph. Toen ik via exact dezelfde route naar huis ging, was het tijdens de spits en reed ik op de terugreis gemiddeld slechts 20 mph. Was de gemiddelde snelheid tijdens mijn retourrit minder dan, groter dan of precies gelijk aan 30 mph?
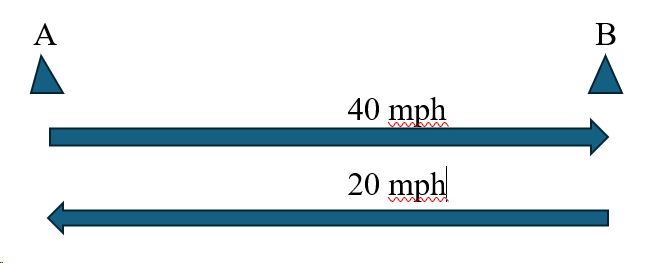
Meestal antwoordt ongeveer 60% van de klas “= 30 mph”. Nog eens 30%, degenen die een klein beetje nadenken, zullen iets zeggen als “Wacht… we moeten weten hoe ver het is tussen huis en werk” of “Hoe lang duurde het heen en weer?”. Deze extra informatie is uiteraard niet nodig. Het grootste deel van de rest zal “<30 mph” suggereren – en dat is goed. En meestal is er iemand die zegt: “Hé, het is precies 26 2/3 mph.”
Niet zo simpele oplossing
Waarom is dit zo moeilijk voor een meerderheid van de studenten? Er wordt ons vaak geleerd om verhoudingen als slechts breuken te beschouwen, maar de ‘rekenkunde’ van verhoudingen is niet simpelweg de rekenkunde van breuken.
Tot nu toe heb ik geweigerd te reageren op enkele opmerkingen die er terecht op wijzen dat er verschillende gemiddelden zijn die in aanmerking kunnen worden genomen, en die mij tot de orde roepen omdat ik niet heb aangegeven welk gemiddelde ik in gedachten had. Ik twijfel er niet aan dat ingenieurs, natuurkundigen of anderen soortgelijke problemen zouden kunnen aanpakken waarbij andere gemiddeles dan de harmonische nuttiger en misschien zelfs redelijker zijn. Maar dit probleem is niet voor hen.
Het gestelde probleem heeft een duidelijke setting. Het is een probleem dat wordt gegeven in een basiscursus algebra. De meeste, zo niet alle, leerlingen in zo’n klas kennen maar één manier om het gemiddelde van twee waarden te vinden: ze bij elkaar optellen en door twee delen. En daarin schuilt de moeilijkheid. Denkt iemand werkelijk dat het specificeren van een tijdgemiddelde waarde versus een padgemiddelde waarde überhaupt iets zou betekenen? Echt? Is dat de zorg van sommige mensen?
Aangezien het voorbeeldprobleem op een geschikt punt in het leerplan wordt voorgesteld (waarvan de oplettende lezer zal vermoeden dat dit een punt is waarna typische afstand/snelheid/tijd-kwesties zijn besproken), denk ik dat we kunnen aannemen dat studenten zullen begrijpen wat wordt bedoeld met snelheid. In feite geeft ongeveer 18 jaar omgaan met bewegende objecten een redelijk goed begrip van wat er met snelheid wordt bedoeld.

Wat is “gemiddeld”?
Maar hoe zit het met de betekenis van “gemiddelde snelheid”? Studenten begrijpen hoe ze de snelheid van een bewegend object moeten berekenen en uit ervaring erkennen ze dat deze berekening in feite een betekenisvolle “gemiddelde” snelheid over tijd en afstand vertegenwoordigt. Dit is het idee dat ze hebben van een gemiddelde snelheid – simpelweg afstand gedeeld door tijd.
Leerlingen weten ook wat een rondrit is: reizen van punt A naar punt B en op een eventueel later tijdstip van punt B naar A. Ze begrijpen wat wordt bedoeld met de gemiddelde snelheid van A naar B, en ook van B naar A Wat ze vaak niet weten, is hoe ze de gemiddelde snelheid van A naar B naar A kunnen vinden, terwijl ze geen afstanden of tijden kennen, maar alleen tarieven.
Dat is de reden waarom velen eenvoudigweg het rekenkundig gemiddelde vinden – ze weten niet wat ze anders moeten doen. Maar deze waarde, hoe redelijk deze voor sommige mensen ook lijkt, komt niet overeen met het begrip van de leerlingen over de gemiddelde snelheid.
Ze zullen inzien dat de algehele gemiddelde snelheid de totale reisafstand is, gedeeld door de totale reistijd. Dit is de meest redelijke interpretatie van de gemiddelde snelheid, ondanks alle andere mogelijke gemiddelden. Misschien niet in alle gevallen de meest bruikbare – misschien niet de favoriet van natuurkundigen. Maar in de situatie en context van dit probleem is dit het meest redelijke.
In feite is dit voor de meeste studenten – en hier kun je de meeste studenten vervangen door de meeste mensen – de enige interpretatie die ze hebben van de gemiddelde snelheid. Ik reken wiskundigen, natuurkundigen of andere professionals die wiskunde gebruiken niet onder ‘de meeste mensen’.
Daarom hebben we hier een probleem in een redelijk eenvoudige context dat redelijk eenvoudig is en waarvan de verklaring algemeen wordt begrepen, maar voor de meeste mensen moeilijk op te lossen zal zijn. En dat is moeilijk te verteren voor de muggenzifterige Quorans (ed. “lezers van Quora”).”
Mijn oplossing
Toen ik het bovenstaande las, was mij wel duidelijk dat de gemiddelde snelheid minder dan 30 moest zijn. Immers: er is langer 20 gereden dan 40 (omdat de afstand hetzelfde is). Dus dit “drukt” het gemiddelde onder de 30.
Maar hoe kon iemand aangeven dat het gemiddelde exact 26 2/3 moest zijn? Het leek alsof je voor die berekening een gegeven miste. Bijvoorbeeld de afstand tussen A en B, of de tijd die voor een van de routes nodig was. Maar bij even doordenken blijkt dat toch niet nodig.
Stel de afstand tussen A en B is x, de totale afstand is dan 2x.
De benodigde tijd voor het afleggen van die afstand is (x/40 + x/20), ofwel 3x/40.
De gemiddelde snelheid over de totale afstand is dan 2x/(3x/40), ofwel 80x/3x en dat is 80/3 en dat is weer 26 2/3.
QED
Wat zegt AI?
Ik heb het probleem ook voorgelegd aan ChatGPT en dit was het antwoord:





